An Assortment of Sorting Algorithms, Part 1

For many reasons, sorting algorithms are an integral topic of any computer science course. Firstly, they are immensely useful from a practical point of view — both directly, when trying to sort some data, and indirectly, by enabling or improving other, more advanced algorithms. Secondly, the wide variety of sorting algorithms is an ideal tool to understand critical concepts such as space and time complexity, notation, recursion, and algorithm analysis.

While modern programming languages and libraries take care of choosing the appropriate sorting algorithm for you, it is still necessary to have at least a basic understanding of what is happening ‘under the hood’. In this series of posts, we will explore a select few algorithms, and implement them in C++.

Heap Sort

The underlying principle of heap sort is the following:

1. Identify the largest element of the (sub-)array.
2. Move it to the very end.
3. Exclude the last (now highest remaining) element by shortening the sub-array.
4. Repeat.

This process hinges on how fast we can isolate the largest member of an array. If we can do it in constant time, then the whole algorithm takes place in , as we simply carry out a constant number of operations at each iteration over the length of the array. If, on the contrary, finding the largest element takes, say, linear time, we are stuck with an algorithm.

So, what is an efficient way to find the highest value in an array? Naively, one might assume that we would need to sort the array in the first place. This, however, is not required. Moving the largest value to the first element of the array is a weaker property, so to say, than ordering the whole array. In the former case, we don’t care what the actual order of all the other values is. So it should not come as a surprise that the former case can be accomplished in a more efficient manner than the latter (sorting the whole sub-array repeatedly).

The extraction of the largest value relies on a so-called max-heap. A max-heap is a special instance of a heap — a binary tree. The ‘max’ qualifier identifies a tree with the property that the value of every parent node is larger than the value of either of its two children. Naturally, the largest value in a max-heap will be located at the root node.

If we associate our sub-array to a heap, we can ensure that at each iteration the heap is a max-heap, and hence extract the largest value from the root. Luckily, it turns out that ‘max-heapifying’ a heap is a procedure that can be accomplished in logarithmic time! Therefore, the combination of such a procedure and a loop over the length of the original array leads to a time cost! And that’s as good as it gets in the general case.

How it Works

First, let’s draw the correspondence between a heap and the array to be sorted:

Our array on the left, and the associated heap on the right. The heap is built by arranging the array elements consecutively into layers of 1, 2, 4, 8, … elements. Each parent has at most two children.

The above heap is clearly not a max-heap. How would we go about turning it into one? The property that needs to be satisfied is that each parent node holds a value larger than those of its two children. Hence, we could iterate over all nodes and check whether this is true. If not, we simply exchange the offending numbers. In fact, we don’t even need to iterate over all nodes, only those that have children, i.e. all with the exception of leaves. For every node, we check whether its left child and/or right child is larger. If yes, we exchange the values of the parent and of the larger of the two children. Furthermore, while the exchange will lead to our criterion being satisfied for that particular parent and child nodes, it might upset the max-heap property of the whole branch. Hence, if we exchange the values of a parent and a child, we should reiterate the procedure with the offending, now swapped, child.

For example, let’s consider the node number 1 with the value 11. We check whether its left child or its right child is larger. We find that the left child (node 3), indeed, is, having a value of 14. We swap the values of nodes 1 and 3. We then move down a level, and repeat this procedure for the offending node 3. Its children are nodes 7 and 8, both of which are smaller. As these are the leaves of the tree, we stop the recursion here. Let us call this procedure max_heapify().

Repeating this procedure for every non-leaf (internal) node will turn our heap into a max-heap. Each call to max_heapify() costs us at most two comparisons and one swap, a constant number of operations. If a swap does occur, and we need to recursively call max_heapify() on the child node every time, we are faced with at most calls, as there are up to levels in the heap. Thus, the cost of max_heapify() is .

There are internal nodes. Consider a complete binary tree such that every level is completely filled. As each level contains a number of nodes equal to a power of two, the last level (made up of all the leaves) will contain as many nodes as all previous levels combined, plus one. In other words, the number of leaves of a complete binary tree is , and the number of internal nodes is . Let’s consider a tree of 7 nodes. The above would lead to 3 internal nodes and 4 leaves. If we now add one more element (), we necessarily turn one of the leaves into an internal node, and indeed is equal to 4. The number of leaves remains the same (we added one leaf, but we turned another leaf into an internal node). Adding yet another node should not increase the number of internal nodes, just the number of leaves. One can easily verify that the above expression holds true in this case as well.

All in all, to turn our heap into a max-heap, we need to call the procedure max_heapify() exactly times, once for each internal node. If we call this the build_max_heap() procedure, we immediately see that its cost scales with the number of array elements as .

---

Once the array is reordered, upon calling build_max_heap(), in such a way as to correspond to a max-heap, we can proceed with the sorting as described previously:

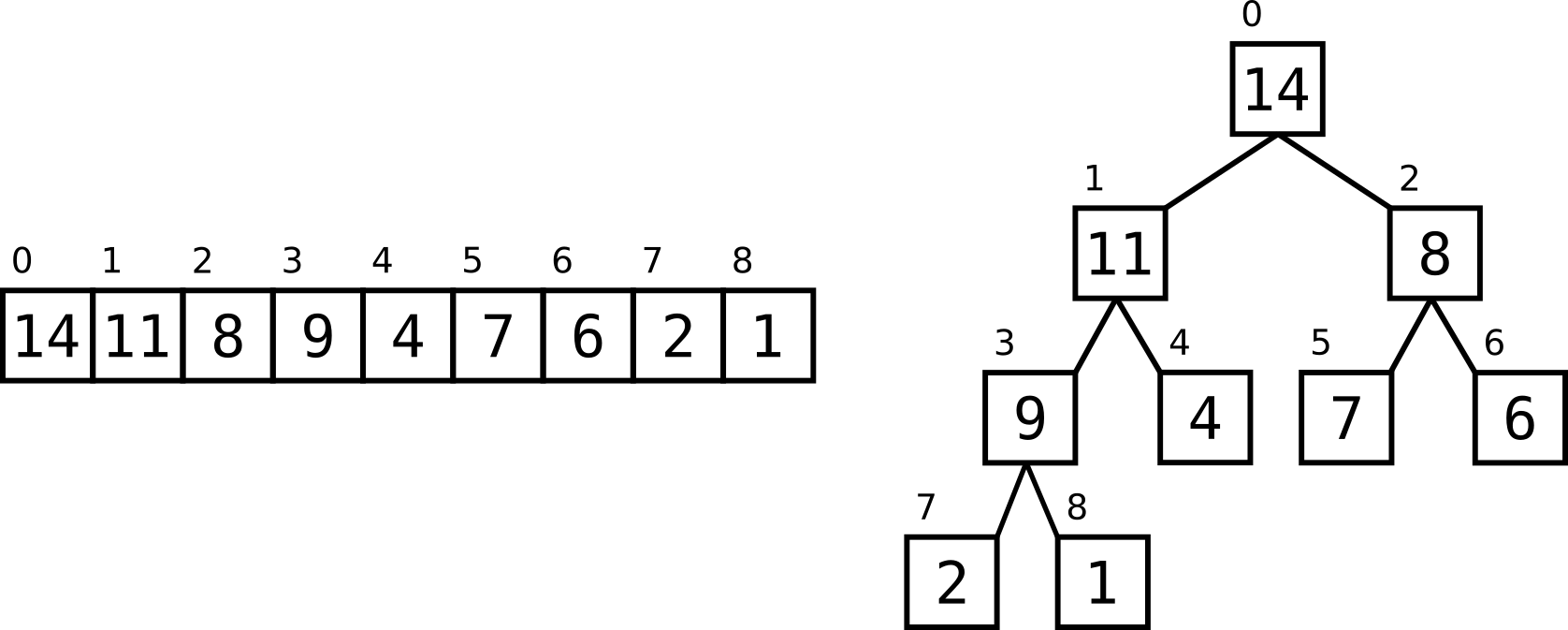
We take the largest element and move it to the end of the array by swapping the first and the last element. We shorten the length of the heap by one:

Node 0 holds a value smaller than either of its children. Node 1 is the larger of the two, so we swap the values of node 0 and node 1. The greyed out array elements are already sorted and thus ignored.

and call the max_heapify() procedure on the first element, the only one possibly upsetting the max-heap property in the shortened heap:

We recursively follow down the branch, focusing on node 1 now. Node 3 is the larger of the children of node 1, a swap and a recursive call take place.

Node 3 only has one child now, and holds a smaller value, thus we swap them again.

We have reached the bottom of the heap, and have achieved the max-heap property. The largest value is held by the rood node.

We swap the last value of our current heap with the value in the root node, and shorten the heap by one,
… and so on and so forth …

until we are left with a heap of length one, at which point the array is necessarily sorted in ascending order. This procedure is hence the heap_sort() function.

Implementation

The implementation of heap_sort() will, therefore, look like this:

template <class T>
void heap_sort(std::vector & vec)
{
    build_max_heap(vec);
    int heap_size = vec.size();
    for (int i = vec.size() - 1; i > 0; --i)
    {
        std::swap(vec[i], vec[0]);
        --heap_size;
        max_heapify(vec, 0, heap_size);
    }
}

As discussed above, the heap_sort() first builds a max-heap via the build_max_heap() function. Then we iterate over each element starting from the end of the array. We swap the first array element (the largest value) with the element at the end of the heap. This done, we reduce the size of the heap, and call max_heapify() on the newly swapped element to ensure the max-heap property in the following iteration.

The build_max_heap() function simply loops over the first half of the array values and repeatedly calls max_heapify() on each element:

template <class T>
void build_max_heap(std::vector & vec)
{
    int heap_size = vec.size();
    for (int i = vec.size() / 2 - 1; i >= 0; --i)
    {
        max_heapify(vec, i, vec.size());
    }
}

All the magic is thus happening inside the max_heapify() routine:

template <class T>
void build_max_heap(std::vector & vec, int i, int heap_size)
{
    int l{ left(i) };
    int r{ right(i) };
    int largest{ 0 };

    if (l < heap_size && vec[l] > vec[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }

    if (r < heap_size && vec[r] > vec[largest])
    {
        largest = r;
    }
    
    if (largest != i)
    {
        std::swap(vec[i], vec[largest]);
        max_heapify(vec, largest, heap_size);
    }
    return;
}

We first find the index of the node holding the largest value among the current node and its two children. If it’s not the current node that holds the largest value, we swap values with the node that does. Finally, as this swapping might upset the max-heap property of the child nodes, we recursively call max_heapify() on the relevant child node. The left() and right() procedures are just helper functions that return the index of the left and the right child node, respectively:

int left(int i) { return 2 * i + 1 }
int right(int i) { return 2 * i + 2 }

---

In conclusion, heap sort is a fast sorting algorithm that sorts an array in place (no extra memory required), and does so in time. The implementation provided here assumes the array is in the form of a standard library vector, but it can trivially be generalized for other containers as well. Personally, what I find the most fascinating about heap sort is how a seemingly unrelated data structure (a heap, a binary tree) can be exploited to achieve such an elegant solution to the sorting problem.

---

For the sake of convenience, the whole header file is reproduced below:

#pragma once
#include <algorithm>
#include <vector>

int left(int i) { return 2 * i + 1 }
int right(int i) { return 2 * i + 2 }

template <class T>
void build_max_heap(std::vector & vec, int i, int heap_size)
{
    int l{ left(i) };
    int r{ right(i) };
    int largest{ 0 };

    if (l < heap_size && vec[l] > vec[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }

    if (r < heap_size && vec[r] > vec[largest])
    {
        largest = r;
    }
    
    if (largest != i)
    {
        std::swap(vec[i], vec[largest]);
        max_heapify(vec, largest, heap_size);
    }
    return;
}

template <class T>
void build_max_heap(std::vector & vec)
{
    int heap_size = vec.size();
    for (int i = vec.size() / 2 - 1; i >= 0; --i)
    {
        max_heapify(vec, i, vec.size());
    }
}

template <class T>
void heap_sort(std::vector & vec)
{
    build_max_heap(vec);
    int heap_size = vec.size();
    for (int i = vec.size() - 1; i > 0; --i)
    {
        std::swap(vec[i], vec[0]);
        --heap_size;
        max_heapify(vec, 0, heap_size);
    }
}